Placage de texture (2/2) Par Xavier Michelon

Nous avons déjà parlé des normales au cours du tutoriel concernant l’éclairage, mais nous avons en fait détourné le problème en utilisant comme objets 3D des primitives glut dont les normales étaient déjà mises en place. Aujourd’hui nous allons voir en détail comment définir une normale.

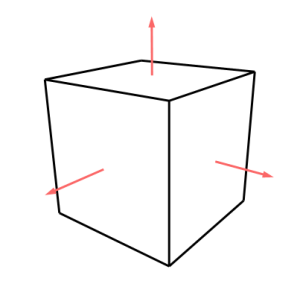
Les algorithmes d’éclairage ont besoin de connaître l’orientation des faces d’un objet. Pour cela, ils mettent en jeu la notion de normale, un vecteur perpendiculaire au polygone considéré (figure 2). Bien sûr, en connaissant les points constituant un polygone, il est possible de calculer un vecteur normal à ce polygone, mais ce calcul est coûteux, et sauf convention implicite dans l’ordre des sommets, il ne permet pas de déterminer automatiquement les faces avant et arrière du polygone. C’est pourquoi il nous faut spécifier les vecteurs normaux.

Figure 2 : un cube et les normales de ses faces

Figure 3 : deux sphères, avec et sans lissage des faces

En OpenGL, on n’associe pas les normales aux polygones mais aux sommets, car cela permet de créer des effets de lissage sur les surfaces courbes (figure 3). Nous aurons l’occasion d’appliquer le lissage la prochaine fois. La spécification des normales se fait comme d’habitude grâce à un système de normale active définie avec la fonction

glNormal3f(float x,float y,float z);

Dans notre cas, chacun des sommets d’une face se voit affecter la même normale, et donc la définition d’une face de notre cube se fait grâce à une portion de code du type :

glBegin(GL_POLYGON);
 glNormal3f(0.0,0.0,1.0); 
 glTexCoord2f(0.0,1.0);   glVertex3f(-0.5, 0.5, 0.5);
 glTexCoord2f(0.0,0.0);   glVertex3f(-0.5,-0.5, 0.5);
 glTexCoord2f(1.0,0.0);   glVertex3f( 0.5,-0.5, 0.5);
 glTexCoord2f(1.0,1.0);   glVertex3f( 0.5, 0.5, 0.5);
glEnd();

Attention, même si à priori les vecteurs (0,0,1) et (0,0,2) pointent dans la même direction, il est important pour l’algorithme d’éclairage que les vecteurs normaux aient une longueur de 1.