Tiu unua ekzemplo ebligis vin kompreni la nocion de sistemo de Lindenmayer, eble sen ekkonscii kiel ni uzos tion
konkrete kun la testudo.
Ja tie tio estiĝas interesa: Ĉiu vorto tiel konstruita nur havas propran signifon. Oni tiam kroĉos al ĉiu litero de la
sinsekvo, komandon rulotan de la testudo, por tiel generi desegnojn 2D aŭ 3D.
- F : Moviĝi je unu unueca paŝo (
 V )
V )
- + : Turniĝi maldekstren je angulo α (
 S).
S).
- - : Turniĝi dekstren je angulo α (
 S).
S).
- & : Pivoti al malsupro je angulo α (
 S).
S).
- ^: Pivoti al supro je angulo α (
 S).
S).
- \: Ruliĝi maldekstren je angulo α (
 S).
S).
- ∕: Ruliĝi dekstren je angulo α (
 S).
S).
- |: Efektivigi duonturniĝon. En XLogo: dn 180
Ni prenu por ekzemplo α = 90 kaj unuecan moviĝon je 10 testudpaŝojn; jen:
|
|
|
|
|
|
|
|
|
| Simbolo | F | + | - | & | ^ | \ | ∕ | | |
|
|
|
|
|
|
|
|
|
| Komando XLogo | an 10 | mdn 90 | dn 90 | malsupren 90 | supren 90 | mdfn 90 | dfn 90 | dn 180 |
|
|
|
|
|
|
|
|
|
| |
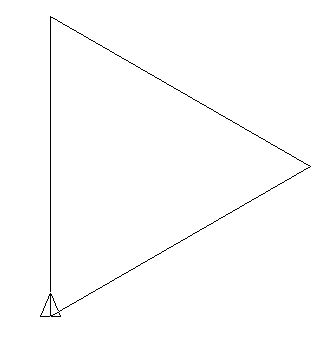
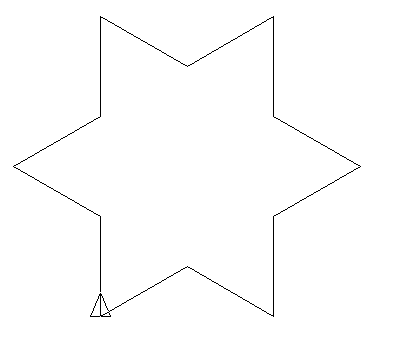
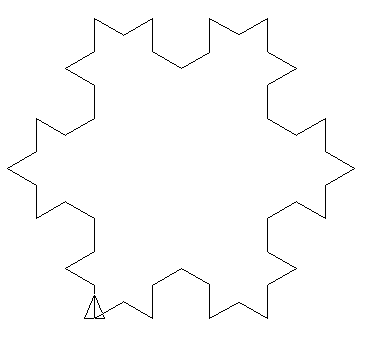
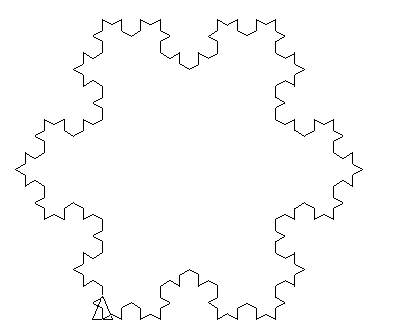
Konsideru la L-sistemon:
- Komenca stato: F --F --F --
- Produkta regulo: F → F + F --F + F
- Angulo α = 60∘, la unuecan paŝon oni dividu per 3 je ĉiu iteracio.
Unuaj iteracioj:
Programo en Logo:
por neĝero :p
provizu "unuo 300 / potencon 3 :p-1
ripetu 3 [F :p-1 td 120]
fino
por F :p
se :p=0 [an :unuo haltu]
F :p-1 mdn 60 F :p-1 dn 120 F :p-1 md 60
F :p-1
fino
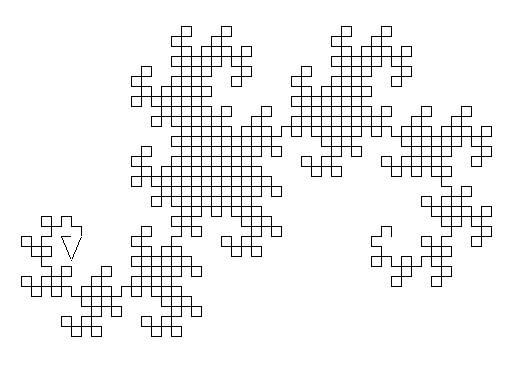
Ni interesiĝu pri la jena L-sistemo:
- Komenca stato: F - F - F - F
- Produkta regulo: F → F - F + F + FF - F - F + F
Jen la unuaj reprezentoj uzante α = 90 kaj alĝustigante la unuecan paŝon tiel ke la figuro havu ĉiam la saman
amplekson:
Tre facilas do krei la programon Logo ebligantan generi tiujn desegnojn:
# p indikas l’ iteracion
por koch :p
# Je ĉiu iteracio, la unueca distanco dividatas per 4
# Ĉi tie, la fina figuro havos amplekson 600x600 maksimume
provizu "unuo 300 / potencon 4 :p-1
ripetu 3 [F :p-1 tg 90] F :p-1
fino
# La ĉeno reskribada
por F :p
se :p=0 [an :unuo haltu]
F :p-1 mdn 90 F :p-1 dn 90 F :p-1 dn 90
F :p-1 F :p-1 mdn 90 F :p-1 mdn 90 F :p-1 dn 90 F :p-1
fino
- Komenca stato: F
- Produkta regulo:
por a :p
se :p=0 [an :unuo haltu]
a :p-1 mdn 90 b :p-1 mdn 90
fino
por b :p
se :p=0 [an :unuo haltu]
dn 90 a :p-1 dn 90 b :p-1
fino
por dragono :p
provizu "unuo 300 / 8 / :p
a :p
fino
La sekva ekzemplo estas la kurbo de Hilbert en la spaco; ĝi estas kurbo kun la atributo plenigi tute kubon kiam oni
pligrandigas la nombron de iteracioj .
Jen la rilata sistemo:
- Komenca stato: A
- Angulo α = 90∘, dividu la unuecan longon per du je ĉiu iteracio.
- Produkta regulo:
|
A → B - F + CFC + F - D&F^D - F + &&CFC + F + B∕∕ |
B → A&F^CFB^F^D^^ - F - D^|F^B|FC^F^A∕∕ |
C →|D^|F^B - F + C^F^A&&FA&F^C + F + B^F^D∕∕ |
D →|CFB - F + B|FA&F^A&&FB - F + B|FC∕∕ |
|
|
por hilbert :p
ev perspektive
provizu "unuo 400 / potencon 2 :p
linia_difino sdikp :unuo/2
a :p
linia_difinhalto
tridimensie_vidigu
fino
por a :p
se :p=0 [haltu]
b :p-1 dn 90 an :unuo mdn 90 c :p-1 an :unuo c :p-1
mdn 90 an :unuo dn 90 d :p-1 malsupren 90 an :unuo supren 90 d :p-1
dn 90 an :unuo mdn 90 malsupren 180 c :p-1 an :unuo c :p-1
mdn 90 an :unuo mdn 90 b :p-1 dfn 180
fino
por b :p
se :p=0 [haltu]
a :p-1 malsupren 90 an :unuo supren 90 c :p-1 an :unuo b :p-1 supren 90
an :unuo supren 90 d :p-1 supren 180 dn 90 an :unuo dn 90 d :p-1 supren 90
dn 180 an :unuo supren 90 b :p-1 dn 180 an :unuo c :p-1 supren 90 an :unuo
supren 90 a :p-1 dfn 180
fino
por c :p
se :p=0 [haltu]
dn 180 d :p-1 supren 90 dn 180 an :unuo supren 90 b :p-1 dn 90 an :unuo mdn 90
c :p-1 supren 90 an :unuo supren 90 a :p-1 malsupren 180 an :unuo a :p-1 malsupren 90
an :unuo supren 90 c :p-1 mdn 90 an :unuo mdn 90 b :p-1 supren 90 an :unuo supren 90
d :p-1 dfn 180
fino
por d :p
se :p=0 [haltu]
dn 180 c :p-1 an :unuo b :p-1 dn 90 an :unuo mdn 90 b :p-1 dn 180
an :unuo a :p-1 malsupren 90 an :unuo supren 90 a :p-1 malsupren 180 an :unuo
b :p-1 dn 90 an :unuo mdn 90 b :p-1 dn 180 an :unuo c :p-1 dfn 180
fino
Jen l’ unuaj iteracioj:
 V )
V )
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 V )
V )
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).
 S).
S).