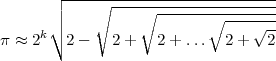
Oni povas akiri proksimumon de la nombro π per la formulo:
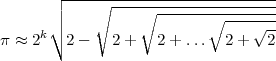
La formulo konsistas el la esprimo 2 +  kiu estas klare rekursiva, de kie la programo
jena:
kiu estas klare rekursiva, de kie la programo
jena:
Oni akiris la 5 unuajn decimalojn! Se oni deziras pli, necesos forigi kelkajn kalkulerarojn pro ne precize kalkuli la koncernitajn kvadrataj radikojn. Por tio ni pligrandigos la nombron de decimaloj per la primitivo decimalojn_provizu.
Kaj nun oni akiras 39 decimalojn...